Condensadores
Básicamente un condensador es un dispositivo capaz de almacenar energía en forma de
campo eléctrico. Está formado por dos armaduras metálicas paralelas (generalmente de
aluminio) separadas por un material dieléctrico.
Tiene una serie de características tales como capacidad, tensión de trabajo, tolerancia
y polaridad, que deberemos aprender a distinguir.
En la versión más sencilla del condensador, no se pone nada entre las armaduras y se las
deja con una cierta separación, en cuyo caso se dice que el dieléctrico es el aire.
• Capacidad: Se mide en Faradios (F), aunque esta unidad resulta tan grande que
se suelen utilizar varios de los submúltiplos, tales como microfaradios (µF=10-6 F),
nanofaradios (nF=10-9 F) y picofaradios (pF=10-12 F).
• Tensión de trabajo: Es la máxima tensión que puede aguantar un condensador,
que depende del tipo y grosor del dieléctrico con que esté fabricado. Si se supera
dicha tensión, el condensador puede perforarse (quedar cortocircuitado) y/o
explotar. En este sentido hay que tener cuidado al elegir un condensador, de forma
que nunca trabaje a una tensión superior a la máxima.
• Tolerancia: Igual que en las resistencias, se refiere al error máximo que puede
existir entre la capacidad real del condensador y la capacidad indicada sobre su
cuerpo.
• Polaridad: Los condensadores electrolíticos y en general los de capacidad superior
a 1 µF tienen polaridad, eso es, que se les debe aplicar la tensión prestando
atención a sus terminales positivo y negativo. Al contrario que los inferiores a 1µF, a
los que se puede aplicar tensión en cualquier sentido, los que tienen polaridad
pueden explotar en caso de ser ésta la incorrecta.
Tipos de Condensadores
Vamos a mostrar a continuación una serie de condensadores de los más típicos que se
pueden encontrar. Todos ellos están comparados en tamaño a una moneda española de
25 Ptas. (0.15 €).
1. Electrolíticos. Tienen el dieléctrico formado por papel impregnado en electrolito.
Siempre tienen polaridad, y una capacidad superior a 1 µF. Arriba observamos
claramente que el condensador nº 1 es de 2200 µF, con una tensión máxima de
trabajo de 25v. (Inscripción: 2200 µ / 25 V).
Abajo a la izquierda vemos un esquema de este tipo de condensadores y a la
derecha vemos unos ejemplos de condensadores electrolíticos de cierto tamaño, de
los que se suelen emplear en aplicaciones eléctricas (fuentes de alimentación,
<La web de Abel/Documentación técnica> Página 1 de 7
etc...)
2. Electrolíticos de tántalo o de gota. Emplean como dieléctrico una finísima película
de óxido de tantalio amorfo, que con un menor espesor tiene un poder aislante
mucho mayor. Tienen polaridad y una capacidad superior a 1 µF. Su forma de gota
les da muchas veces ese nombre.
3. De poliester metalizado MKT. Suelen tener capacidades inferiores a 1 µF y
tensiones de trabajo a partir de 63v. Más abajo vemos su estructura: dos láminas de
policarbonato recubierto por un depósito metálico que se bobinan juntas. Aquí al
lado vemos un detalle de un condensador plano de este tipo, donde se observa que
es de 0.033 µF y 250v. (Inscripción: 0.033 K/ 250 MKT).
4. De poliéster. Son similares a los anteriores, aunque con un proceso de fabricación
algo diferente. En ocasiones este tipo de condensadores se presentan en forma
plana y llevan sus datos impresos en forma de bandas de color, recibiendo
comúnmente el nombre de condensadores "de bandera". Su capacidad suele ser
como máximo de 470 nF.
5. De poliéster tubular. Similares a los anteriores, pero enrollados de forma normal,
sin aplastar.
<La web de Abel/Documentación técnica> Página 2 de 7
6. Cerámico "de lenteja" o "de disco". Son los cerámicos más corrientes. Sus
valores de capacidad están comprendidos entre 0.5 pF y 47 nF. En ocasiones
llevan sus datos impresos en forma de bandas de color.
Aquí abajo vemos unos ejemplos de condensadores de este tipo.
7. Cerámico "de tubo". Sus valores de capacidad son del orden de los picofaradios
y generalmente ya no se usan, debido a la gran deriva térmica que tienen (variación
de la capacidad con las variaciones de temperatura).
2.4 - Identificación del valor de los condensadores
Codificación por Bandas de Color
Hemos visto que algunos tipos de condensadores llevan sus datos impresos codificados
con unas bandas de color. Esta forma de codificación es muy similar a la empleada en las
resistencias, en este caso sabiendo que el valor queda expresado en picofaradios (pF).
Las bandas de color son como se observa en esta figura:
<La web de Abel/Documentación técnica> Página 3 de 7
• En el condensador de la izquierda vemos los siguientes datos:
verde-azul-naranja = 56000 pF = 56 nF (recordemos que el "56000" está
expresado en pF). El color negro indica una tolerancia del 20%, tal como veremos
en la tabla de abajo y el color rojo indica una tensión máxima de trabajo de 250v.
• En el de la derecha vemos:
amarillo-violeta-rojo = 4700 pF = 4.7 nF. En los de este tipo no suele aparecer
información acerca de la tensión ni la tolerancia.
Código de colores en los Condensadores
COLORES Banda 1 Banda 2 Multiplicador Tensión
Negro -- 0 x 1
Marrón 1 1 x 10 100 V.
Rojo 2 2 x 100 250 V.
Naranja 3 3 x 1000
Amarillo 4 4 x 104 400 V.
Verde 5 5 x 105
Azul 6 6 x 106 630 V.
Violeta 7 7
Gris 8 8
Blanco 9 9
COLORES Tolerancia (C > 10
pF) Tolerancia (C < 10 pF)
Negro +/- 20% +/- 1 pF
Blanco +/- 10% +/- 1 pF
Verde +/- 5% +/- 0.5 pF
Rojo +/- 2% +/- 0.25 pF
Marrón +/- 1% +/- 0.1 pF
Codificación mediante letras
Este es otro sistema de inscripción del valor de los condensadores sobre su cuerpo. En
<La web de Abel/Documentación técnica> Página 4 de 7
lugar de pintar unas bandas de color se recurre también a la escritura de diferentes
códigos mediante letras impresas.
A veces aparece impresa en los condensadores la letra "K" a continuación de las letras; en
este caso no se traduce por "kilo", o sea, 1000 sino que significa cerámico si se halla en
un condensador de tubo o disco.
Si el componente es un condensador de dieléctrico plástico (en forma de paralelepípedo),
"K" significa tolerancia del 10% sobre el valor de la capacidad, en tanto que "M"
corresponde a tolerancia del 20% y "J", tolerancia del 5%.
LETRA Tolerancia
"M" +/- 20%
"K" +/- 10%
"J" +/- 5%
Detrás de estas letras figura la tensión de trabajo y delante de las mismas el valor de la
capacidad indicado con cifras. Para expresar este valor se puede recurrir a la colocación
de un punto entre las cifras (con valor cero), refiriéndose en este caso a la unidad
microfaradio (µF) o bien al empleo del prefijo "n" (nanofaradio = 1000 pF).
Ejemplo: un condensador marcado con 0,047 J 630 tiene un valor de 47000 pF = 47 nF,
tolerancia del 5% sobre dicho valor y tensión máxima de trabajo de 630 v. También se
podría haber marcado de las siguientes maneras: 4,7n J 630, o 4n7 J 630.
Codificación "101" de los Condensadores
Por último, vamos a mencionar el código 101 utilizado en los condensadores cerámicos
como alternativa al código de colores. De acuerdo con este sistema se imprimen 3 cifras,
dos de ellas son las significativas y la última de ellas indica el número de ceros que se
deben añadir a las precedentes. El resultado debe expresarse siempre en picofaradios pF
.
Así, 561 significa 560 pF, 564 significa 560000 pF = 560 nF, y en el ejemplo de la figura de
la derecha, 403 significa 40000 pF = 40 nF.
Ejemplos de Identificación con Condensadores
...y en esta nueva ocasión vamos a poner a prueba los conceptos explicados
anteriormente. Vamos a presentar una serie de condensadores escogidos al azar del
cajón para ver si sois capaces de identificar sus datos correctamente, ok?
<La web de Abel/Documentación técnica> Página 5 de 7
- 0,047 J 630
- C=47 nF 5%
- V=630 V.
- 403
- C=40 nF
- 0,068 J 250
- C=68 nF 5%
- V=250 V.
- 47p
- C=47 pF
- 22J
- C=22 pF 5%
- 2200
- C=2.2 nF
- 10K +/-10% 400 V
- C=10 nF 10%
- V=400 V
- 3300/10 400 V
- C=3.3 nF 10%
- V=400 V.
- amarillo-violetanaranja-negro
- C=47 nF 20%
- 330K 250V
- C=0.33 µF
- V=250 V.
- n47 J
- C=470 pF 5%
- 0,1 J 250
- C=0.1 µF 5%
- V=250 V.
- verde-azul-naranja
- -negro-rojo
- C=56 nF 20%
- V=250 V.
- µ1 250
- C=0.1 µF
- V=250 V.
- <La web de Abel/Documentación técnica> Página 6 de 7
- 22K 250 V
- C=22 nF
- V=250 V.
- n15 K
- C=150 pF 10%
- azul-gris-rojo y
- marrón-negro-nara
- nja
- C1=8.2 nF
- C2=10 nF
- amarillo-violeta-rojo
- C=4.7 nF
- .02µF 50V
- C=20 nF
- V=50 V.
- amarillo-violeta-rojo,
- rojo-negro-marrón y
- amarillo-violeta-marrón
- C1=4.7 nF
- C2=200 pF
- C3=470 pF
Archivo descargado de "La web de Abel". Archivos de este tipo los tienes disponibles en
cualquiera de mis web. Si te interesan, aquí tienes los enlaces:
http://www.humano.ya.com/webabelnet
http://home.tele2.es/webabel
<La web de Abel/Documentaci




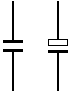
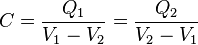
 : Capacitancia o capacidad
: Capacitancia o capacidad : Carga eléctrica almacenada en la placa 1.
: Carga eléctrica almacenada en la placa 1. : Diferencia de potencial entre la placa 1 y la 2.
: Diferencia de potencial entre la placa 1 y la 2.
 , almacenada por un condensador con capacidad
, almacenada por un condensador con capacidad  Donde
Donde  es la carga inicial.
es la carga inicial. 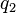 es la carga final.
es la carga final. 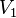 es la tensión inicial.
es la tensión inicial. 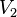 es la tensión final.
es la tensión final.



 ) por la
) por la 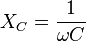
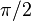 ) respecto a la tensión aplicada.
) respecto a la tensión aplicada.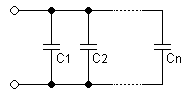
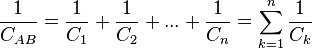
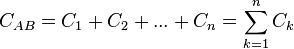
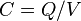 ) la suma de capacidades será simplemente la suma algebraica.
) la suma de capacidades será simplemente la suma algebraica.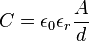
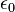 es la
es la 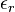 es la constante dieléctrica o permitividad relativa del material
es la constante dieléctrica o permitividad relativa del material 
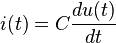




 . Si se representa el
. Si se representa el 







